A sturdy wheel depends on a sturdy rim. The rim serves several purposes: it seats the tire, keeps the spokes under tension, distributes external forces to the spokes, and (in the case of rim brakes) stops the bicycle. From a structural standpoint, we mostly care about the stiffness of the rim, or its ability to resist changes in shape. The rim has a different stiffness for each of the ways it can change shape.
The axial stiffness resists changes in the total length (circumference) of the rim. It determines how much the total rim circumference changes when all the spokes are evenly tightened or the tire is inflated. Other than these two cases, it doesn't really play an important role because it's so much larger than the other stiffness (you can easily bend a rim over you knee and see the lateral deformation, but you couldn't pull inwards on the rim and expect to notice any real change in circumference).
The other three deformation modes are illustrated below on a short rim section:
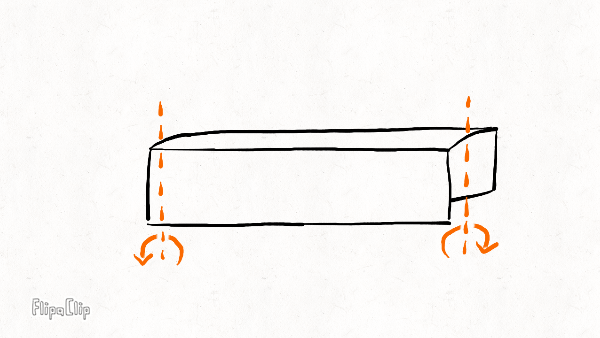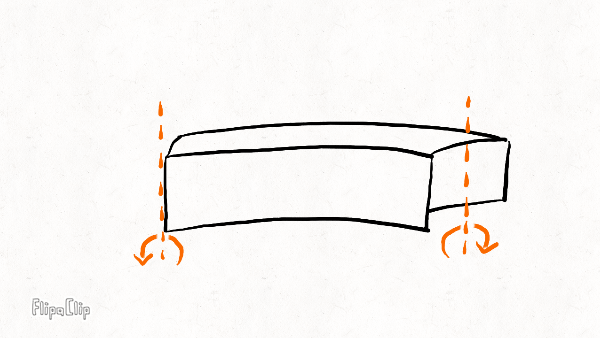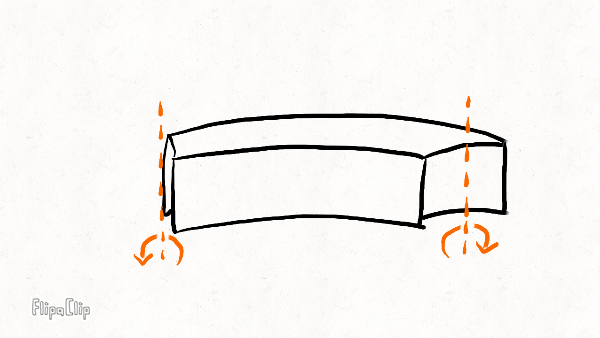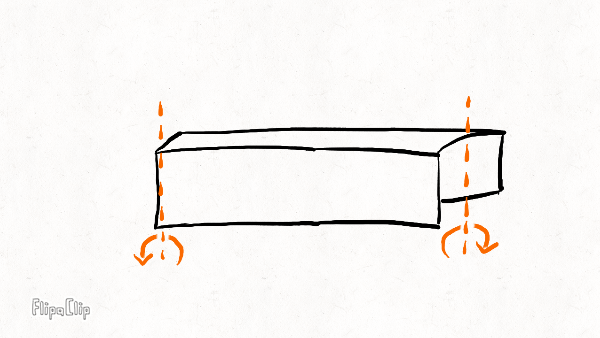
Radial bending
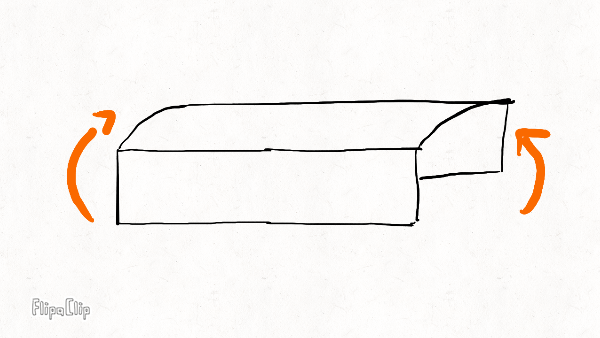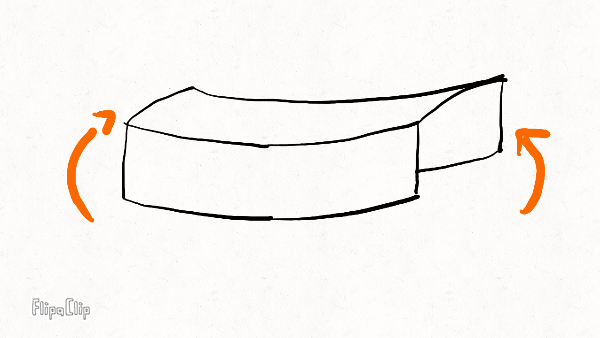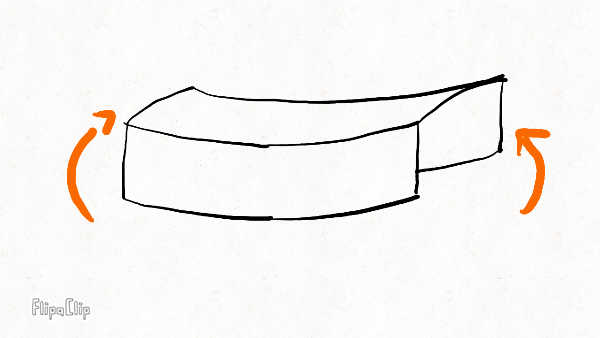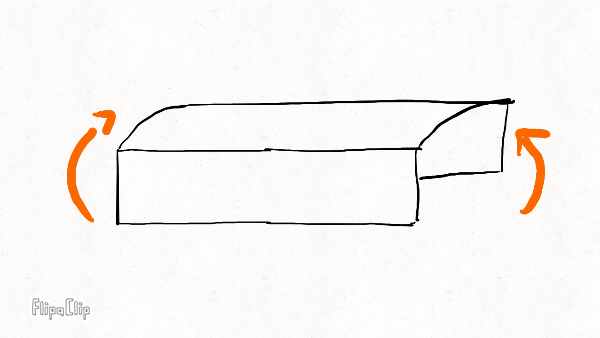
Lateral bending
Torsion
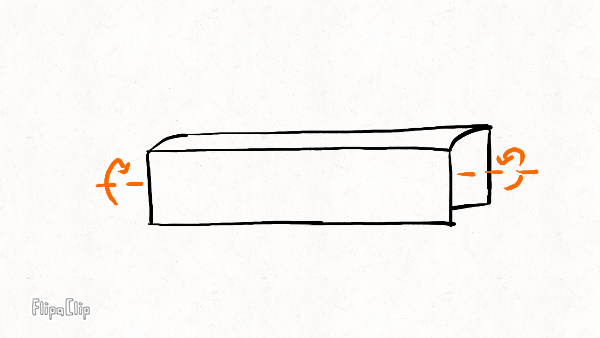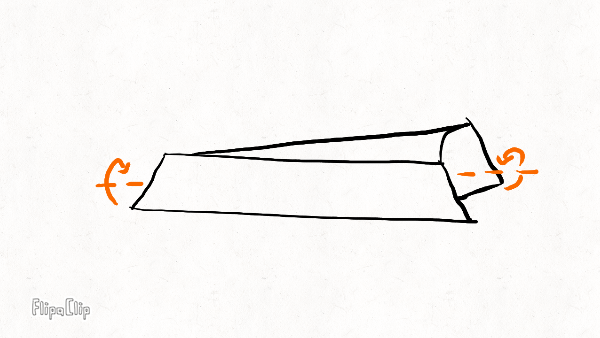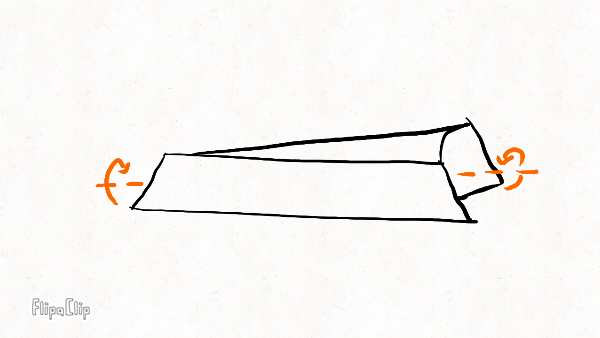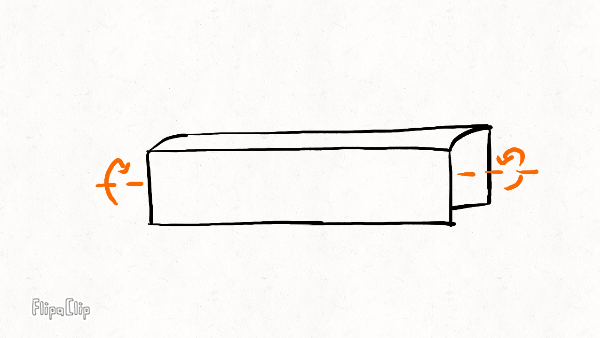
The radial stiffness resists "squashing" of the rim in the vertical plane. It determines how much the rim squashes under weight and how widely the rim distributes force to the spokes underneath the hub. The higher the radial stiffness, the more spokes will share the load and the less likely the bottom spoke is to buckle.
The lateral stiffness resists sideways bending. It controls how much the rim deforms under side forces. Together with the torsional stiffness, it also keeps the rim flat under large spoke tensions.
The torsional stiffness resists twisting of the rim around its circumference. This is not the same as the torsional (or wind-up stiffness) of the wheel, which resists rotation of the rim relative to the hub (around the axle). It also controls how much the rim deforms under side forces. The torsional stiffness is generally much smaller than the lateral stiffness, and because the more flexible mode dominates, it is generally much more important for the overall wheel stiffness than the rim lateral stiffness.
Rim stiffness library
The stiffness properties of the rims below have been measured using the acoustic measurement technique developed by Ford, Peng, and Balogun. The values have been rounded to convenient whole numbers.
Masses are in grams. Stiffness are in N-m^2 (Newton-meters squared). The stiffness can be interpreted as the torque required (measured in Newton-meters) to produce a unit change in curvature (1/meters) in the case of bending, or a unit change in twist rate (radians per meter) in the case of torsion.
| Rim | Size | Mass [g] | Radial | Lateral | Torsional | Notes | Credit |
Notes
[1] The mass of this rim has not been indepedently measured. The calculated stiffnesses are based on the mass provided by the manufacturer. If the true mass is higher than what is listed here, the true stiffness would be correspondingly higher.
Credit
Thanks to the following people who provided me with their rim data:
[GE] Gabriel Ewig, mechanic at Old Goat Gear Exchange in Ithaca, NY.